Le bayésianisme est une approche en statistiques et en épistémologie qui repose sur la théorie des probabilités bayésienne. Cette approche tire son nom du mathématicien Thomas Bayes. Et c'est cette formule de Bayes qui donne au livre son nom "la formule de savoir", puisqu'elle est plus qu'une simple formule dans les statistiques mais toute une approche de pensée.
est la probabilité de l'hypothèse sachant (la probabilité conditionnelle de sachant ).
est la probabilité de sachant (la probabilité conditionnelle de sachant ).
est la probabilité a priori de , c'est-à-dire la probabilité de avant d'avoir les nouvelles informations .
est la probabilité marginale de , c'est-à-dire la probabilité de indépendamment de .
L'approche bayésien
Sans préjugé, aucune conclusion ne peut être tirée. - Lê
"La théorie des probabilités n’est, au fond, que le bon sens réduit au calcul ; elle fait apprécier avec exactitude ce que les esprits justes sentent par une sorte d’instinct, sans qu’ils puissent souvent s’en rendre compte." - Pierre-Simon Laplace (1749-1827)
La conséquence étant que tout modèle de connaissance n'est qu'une croyance à ajuster à chaque fois avec les données empiriques. Donc, tout est subjectif mais ça ne ferait pas que tout opinion est égal.
"Tous les modèles sont faux, certains sont utiles." - George Box
La pure bayésienne et le bayésien pragmatique
La pure bayésienne est la formule "complexe" qui n'est pas si simple à calculer. Du coup, une formule plus simple et rapide est introduit, c'est ce que Lê appelle le bayésien pragmatique.
Problème de l'auto-référence ???
Un problème récurant dans la philosophie est l'auto-référence. Si on prend l'exemple du principe de réfutabilité de Popper, ce principe lui même n'est pas réfutable donc il se contredit. Le bayésianisme aussi a ce défi.
Exemples de problèmes résolus par la formules de Bayes
Le problème des deux enfants
Un père a deux enfant, au moins un d'eux est un garçon. Quelle est la probabilité que le 2ème soit un garçon aussi?
Réponse 1: Le genre du 2ème enfant ne dépend pas du premier donc 1/2.
Réponse 3 (bayésienne): 1/3
Problème de Monty Hall
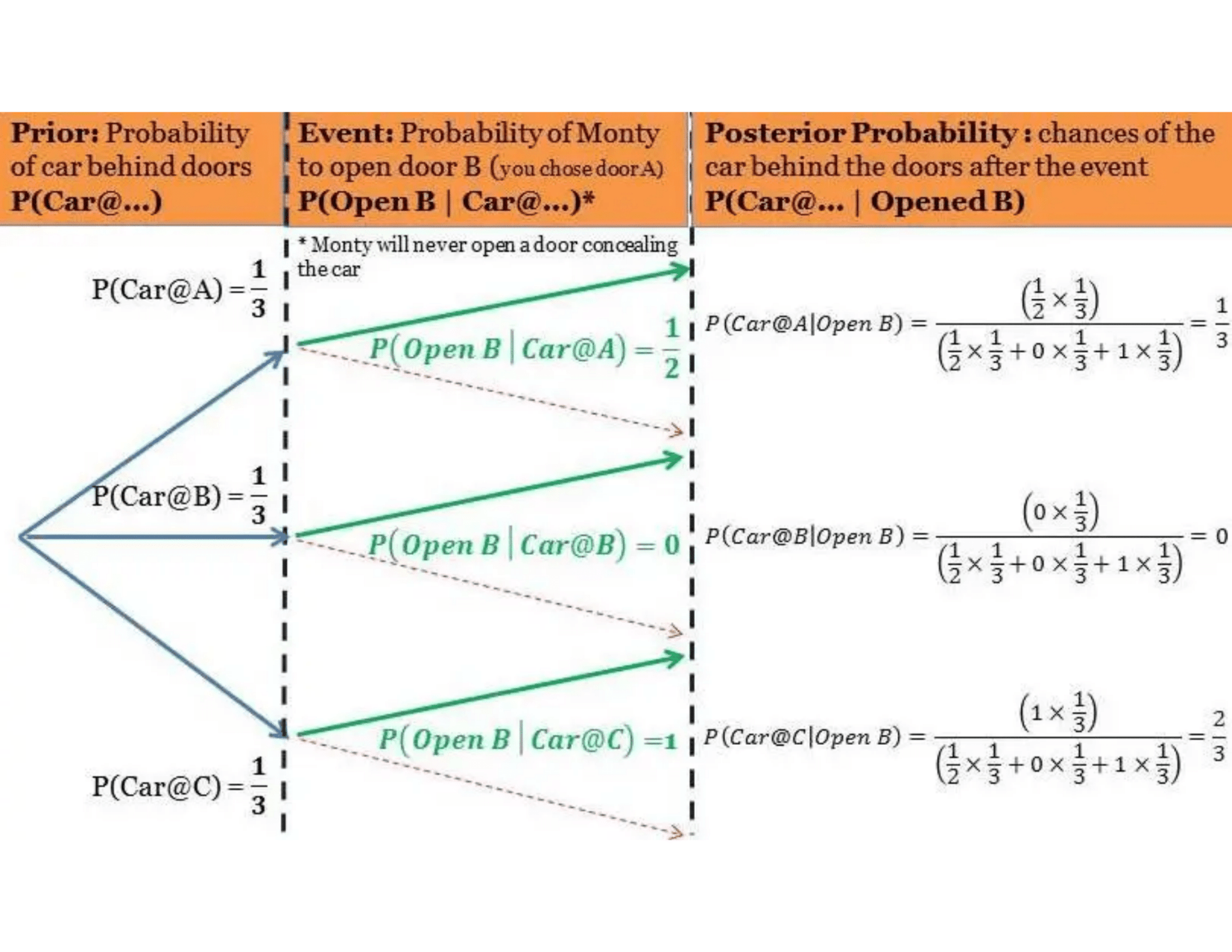
Vous avez 3 portes fermées, derrière l'une d'eux se cache une voiture, les deux autres: rien. Vous choisissez une, vous avez 1/3 de chance à gagner la voiture. L'une des deux autres portes s'ouvre et il y en a rien. Vous avez le choix à choisir l'autre porte ou garder votre choix.
Selon les calculs, si vous changer la porte vous avez 2/3 chance à gagner! C'est vérifié empiriquement et c'est vrai mais ce n'est pas évident intuitivement.
La démonstration est la suivante:
La probabilité que la voiture soit derrière une des portes est a priori 1/3:
Le problème de Linda
Linda a 31 ans. Elle est célibataire, franche et très intelligente. Elle a fait des études de philosophie. Quand elle était étudiante, elle était très concernée par les problèmes de discrimination et de justice sociale, et a aussi participé à des manifestations anti-nucléaires. Qu’est-ce qui est le plus probable ?
Moi personnellement, j'ai choisit la 2ème réponse: car, le fait d'être caissière de banque est le même dans les cas, mais j'aurais penser qu'elle pourrait être féministe. Mais on y réfléchissant, j'ai probablement tort, par ce que la plupart des gens (+80%) ont donné la mauvaise réponse. Et aussi par ce qu'en fait, déjà on ne sait pas la probabilité qu'elle soit caissière de banque, peut être 10%, et celle de devenir féministe peut être 50%. Si on fait la multiplication ça donne 5% ce qui est fortement plus faible que le premier probabilité. Donc avoir deux événement peu probable à la fois est moins probable qu'un d'eux. Mais pourquoi j'avais l'intuition de choisir la 2ème?
Quelque soit la probabilité qu'elle soit féministe ou celle qu'elle soit caissière de banque, on aura toujours P(choix 1) >= P(choix 2).
P[2|Preambule] = P[Feministe|Preambule et Banque] · P[1|Preambule].
La déduction et l'induction
La logique
La logique ou la déduction est ce qu'on utilise largement dans les mathématiques. Elle est complexe et si divers, il y en a plusieurs types.
Lê distingue deux types de logiciens: platonicien, qui croit à une réalité logique où la Vérité est démontrable; et intuitionniste, qui voit les démonstrations mathématiques comme des objets à construire à partir des axiomes suivants les lois de la logique, en y ajoutant le théorème d'incomplétude de Gödel, qui a démontré que certaines théorèmes ne sont pas démontrables ou réfutables.
Du coup, un problème de la logique arrive. « P ou non P » est une tautologie. Si P est vraie, alors « P ou non P » est vraie aussi. Et si P est fausse, alors non P est vraie, et donc « P ou non P » est vraie aussi. Mais il y a une troisième possibilité : le cas où P n’est ni démontrable ni réfutable. On dit alors de P qu’il est indécidable. Du coup, la proposition « P ou non P » est alors indécidable elle aussi.
Logique bayésienne
Il y a une autre logique basée sur le bayésianisme, c'est la logique bayésienne. Elle a ses propres expressions. P(A) = 1 est équivalente à "A est vrai", alors que P(A) = 0 <=> A est faux.
L'implication peut s'écrire: P(A|B)=1 <=> (A=>B)
Or cette expression P(A|B)=1 n'est pas applicable si P(B)=0.
La quantification universelle « ∀xA(x) » se traduit alors par l’identité P[A(x)] = 1, ainsi que la quantification existentielle « ∃xA(x) » se traduit en P[A] > 0.
La conséquence directe d'utiliser la logique bayésienne est que l'évaluation d'une expression ne serait plus binaire mais une probabilité, une crédence qui peut augmenter ou diminuer avec les données ou évidences.
Une autre propriété unique du bayésianisme est la possibilité de combiner plusieurs théories incompatibles et leurs prédictions: Une forêt de modèles incompatibles est plus sage que chacun de ses arbres.
L'induction ou la généralisation
"Toute connaissance dégénère en probabilité; et cette probabilité est plus ou moins grande, en fonction de notre expérience de la vérité ou de la fausseté de notre compréhension, et en fonction de la simplicité ou de la complexité de la question." - David Hume (1711-1776)
Pour Hume, les observations dans le mondes réelles n'impliquent pas des vérités sur le monde. Ce ne sont que des généralisations, mais elles sont utiles pragmatiquement. Ce qui est en accord avec le principe de réfutabilité.
Le principe de réfutabilité de Karl Popper dit qu'une théorie n'est scientifique que si elle réfutable par l'expérience, donc si on peut faire une expérience et déprouver la théorie, c'est qu'elle scientifique, sinon, si je prétends qu'un démon à 4 yeux habite sur le soleil, alors ce ne peut pas être vérifié, donc ce n'est pas une théorie. Mais l'un des superstar de la physique, Einstein, n'avait pas besoin de vérifier sa théorie de relativité, il en croyait tout simplement, par ce qu'il a fait les maths!
Ce n'est pas le cas uniquement pour Einstein et sa théorie de relativité, mais aussi pour la mécanique quantique, la théorie des cordes, l'évolution darwinienne, etc. L'induction est largement utilisée et est importante dans les sciences. Non pas seulement l'induction, mais le fait qu'une seule expérience a réfuté une théorie ne veut pas dire que la théorie est fausse, et les scientifiques y croient encore, parce qu'on peut l'explique par une erreur de l'expérience. Ce qui importe est la crédence de la théorie!
Et pour Lê, ce qui distingue les « sciences » des « pseudo-sciences » par exemple, n’est pas la réfutabilité des hypothèses de ces disciplines, mais la justesse de l’application de la formule de Bayes.
Statistiques fréquentistes et bayésiennes
P-value
Dans les statistiques fréquentistes, il y a une notion très important: la p-value, qui représente la probabilité d'observer des données aussi extrêmes ou plus extrêmes que celles obtenues, sous l'hypothèse nulle. L'hypothèse nulle (H0) est une déclaration initiale selon laquelle il n'y a pas d'effet ou de différence significative. (Par exemple: Les bosons de Higgs n'existent pas). Une petite p-value (typiquement inférieure à un seuil, comme 0,05) suggère que les données sont peu probables sous l'hypothèse nulle, ce qui conduit souvent à rejeter cette hypothèse.
Dans notre exemple si on suppose que les bosons de Higgs n'existent pas, et qu'on trouve par expérience des résultats très improbables, donc on doit rejeter l'H0. Du coup, les bosons de Higgs existent!
La critique de la p-value est sur le choix de la seuil qui est arbitraire, et sur le fait qu'on pourrait rejeter toute théorie si on choisit les bons nombres, ou que parfois on n'a pas tout simplement des données! Mais pire encore, le p-hacking: la manipulation consciente ou inconsciente des procédures statistiques pour obtenir des résultats significatifs (une p-value faible), souvent en testant de multiples hypothèses ou en choisissant des méthodes d'analyse en fonction des résultats observés ou la sélection sélective des données.
Le problème du Soleil d'xkcd
Un exemple trompeur du mal-usage de p-value est le problème du Soleil d'xkcd: Imaginez-vous à Paris. Bob est à Hawaii. Juste avant minuit, il lancera deux dés. S’il tombe sur un double six, il vous dira que le soleil a disparu. Sinon, il vous dira si le soleil a disparu. Minuit sonne. Bob appelle et dit que le soleil a disparu. Que pouvez-vous conclure ?
En utilisant la p-value, si on veut montrer que le soleil est disparu. H0: le soleil n'est pas disparu. On calcule p = 1/6 * 1/6 = 1/36 = 0.028 qui est la probabilité de tomber sur de faces 6 des deux dés. Alors p<0.05 donc on rejette H0. Du coup, le soleil est disparu!
Formule de Bayes
Dans la formule de Bayes, il y a un terme équivalent à la fameuse p-value: P[Data|Theorie]. Cependant, il est crucial de prendre en considération la probabilité à priori P[Théorie].
Et maintenant, l’a priori est là un a priori calculé à partir des données D collectées avant la nouvelle donnée NewData. Donc on va remplacer l’a priori fondamental P[T] par sa crédence actuelle P[T|D] et P[A] par P[A|D].
Si on utilise la formule de Bayes avec le problème précèdent du soleil d'xkcd, on trouve:
avec Vecu est l'ensemble des expériences qu'on avait avec le soleil et les données scientifiques. Vecu=D. Et on a le préjugé P(Soleil|Vécu), qui fait toute la différence.Les préjugés
Selon Lê, il faut avoir des préjugés plutot que dire je ne sais pas, parceque ça serait une occasion pour savoir quand peut on faire confiance à notre intuition ou pas, et parceque notre biais est en fait issue d'un ensemble d'expériences qu'on a vécu même s'il ne reflète pas la réalité! Alors, il vaut mieux d'avoir des préjugés et les mettre à jour avec des nouvelles données que de ne rien penser!
« Douter de tout ou tout croire sont deux solutions également commodes, qui l’une et l’autre nous dispensent de réfléchir » -Poincaré
Une autre raison pour avoir des préjugés est raison est ludique: Se rendre compte qu’une prédiction tombe juste est plaisant, mais découvrir qu’une intuition très convaincante est erronée peut être d’une jouissance exquise! Celui qui n’a jamais vécu l’extase de la découverte d’un fait contre-intuitif ne comprendra jamais cette raison de vivre des scientifiques.
La phrase la plus excitante à entendre en science n’est pas “eurêka”, mais “c’est bizarre” - Isaac Asimov
Or il y a la possibilité d'avoir des préjugés erronées influencées par des biais cognitifs ou par les on-dit plutôt que des données empiriques. Il faut absolument appliquer la formule de Bayes pour calculer la préjugé (l'a priori).
Cryptographie
Chiffre César: décaler les lettres de l'alphabet (par exemple A devient D, B devient E... et ainsi de suite). Il faut essayer 25 fois pour le décoder.
Permutation de lettres, Remplacer A par n'importe quel autre alphabet (26 choix), puis B par un des 25, puis C par un des 24, etc. Il faut 26! essais pour le décoder. C'est un nombre de l'ordre 10^26.
La sécurité et confidentialité de nos technologies de communication est garantie par l’immensité du nombre de codages possibles, et par l’hypothèse selon laquelle tout hacker devra tester une grosse portion de ces codages pour réussir son coup. Cependant, tout ce raisonnement ignore les deux outils de prédilection du bayésien : le préjugé et la formule de Bayes.
Pour décoder un message encrypté par la méthode de substitution par exemple, on peut utiliser des préjugés, voir les lettres les plus utilisées dans la langue, et déterminer ceux qui y correspondent, par la suite si on déchiffre 2 lettres, on peut remplir les lettres vides pour trouver des mots les plus utilisés ou bien les plus probables. Tout ça se repose sur la probabilité sans avoir besoin d'essayer 26! fois.
Confidentialité
Le problème de sondage de l'armée américaine sur la consommation de marijuana.
Pour garder la confidentialité des soldats, on leur demande de répondre honnêtement s'ils ont pile, et dire "oui" si c'était face. Alors les résultats sont: 160 oui, 40 no. On sait que 100 des réponses "oui" aurait "face". Alors on a un préjugé 60% fume, 40% non.
Maintenant pour calculer la probabilité qu'un soldat qui a répondu "oui" fume. On applique la formule:
P[oui] = (P[oui|fume] *P[fume]) + (P[oui|non-fumeur] * P[non-fumeur]) = 0.6 * 1 + 0.5 * 0.4 = 0.8
P[fume|oui] = 0.6 / 0.8 = 0.75
Et intuitivement, si on prend les 160 soldats qui ont répondu "oui", on sait déjà que 60 d'eux ont répondu honnêtement. Les autre 100 qui ont répondu oui, 60% parmi eux fument. Donc (60 + 60) / 160 = 75%
Alors un soldat tiré par hasard a 60% d'être fumeur, mais le fait de participer au sondage et répondre "oui" augmente cette chance à 75%. Mais Il y a un problème de confidentialité des personnes qui ont répondu "non". On sait qu'ils ne fument pas (même si ça semble n'avoir aucun effet mais ça reste un problème de confidentialité).
Pour résoudre ce problème, le sondage sera modifié et il y aura deux pièces à lancer: Dans cette variante, tout soldat a une chance sur deux de répondre honnêtement, une chance sur quatre de répondre oui à cause des lancers de pièces, et une chance sur quatre de répondre non à cause des lancers de pièces.
Faisant les calculs, on aura une crédence de 82 % en le fait qu’un soldat ayant répondu oui au sondage est effectivement un fumeur. Et à l’inverse, une crédence de 33% en le fait qu’un soldat ayant répondu non au sondage fume malgré tout. Donc ça a impacté le degré de confidentialité par les rapports 82/60 et 60/33. Cette perte de confidentialité peut avoir même un rapport de 3 dépendant du préjugé.
Les préjugés de la théorie bayésienne ne sont pas morales. Ce qui est moral sort du domaine bayésien. Mais ces préjugés sont nécessaires dans le cadre du conséquentialisme pour faire le bon choix, scientifiquement, et atteindre des objectifs.
Equilibre de Nash: pierre bat ciseaux
p169

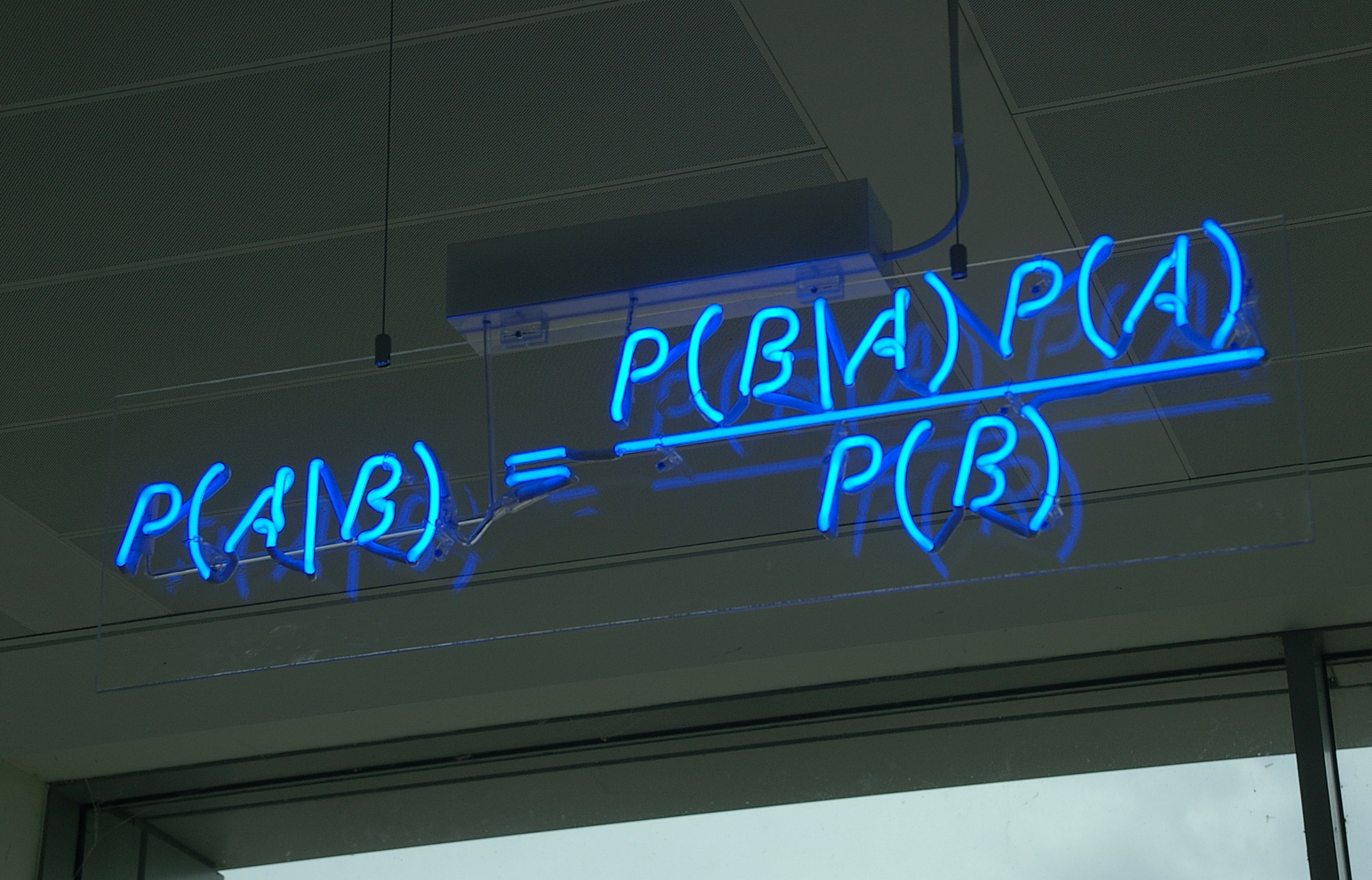








Comments
Post a Comment